1) Gradient, Divergence, Curl and Laplacian

I took the work I’d done 5 yrs ago.

cf) I would inform you the calculation is done in what surface once.

I will use just a picture to explain you Grad, Div, Curl, and Laplacian.

1) Grad

When a scalar function Φ is defined, The gradient of Φ, Grad(Φ), is like below:

$$\nabla\phi\,\,=\,\,\lim_{\int_\,d\tau \to 0}\frac{\int_\,\phi\,d\sigma}{\int_\,d\tau}$$

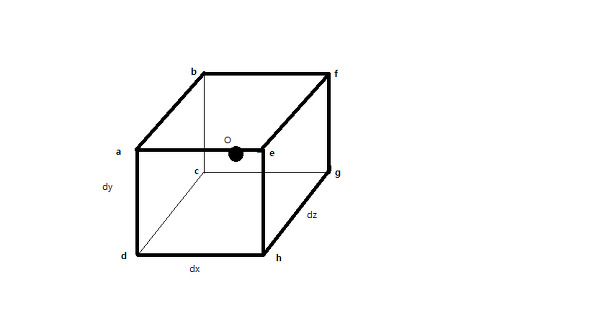
Let us analysis above formula at origin O. ∫φdσ on Cartesian Coordinate for each plane is expressed like below:

$\int_\,\phi\,d\sigma\,\,=$ $\hat{x}[-\iint_{ABCD}^{}(\phi-\frac{\partial \phi}{\partial x} \frac{dx}{2})dydz\,\,\,+\iint_{EFGH}^{}(\phi+\frac{\partial \phi}{\partial x} \frac{dx}{2})dydz]$ $+\,\hat{y}[-\iint_{CDHG}^{}(\phi-\frac{\partial \phi}{\partial y} \frac{dy}{2})dxdz\,\,\,+\iint_{ABEF}^{}(\phi+\frac{\partial \phi}{\partial y} \frac{dy}{2})dxdz]$ $+\,\hat{z}[-\iint_{ADHE}^{}(\phi-\frac{\partial \phi}{\partial z} \frac{dz}{2})dxdy\,\,\,+\iint_{BCGF}^{}(\phi+\frac{\partial \phi}{\partial z} \frac{dz}{2})dxdy]$ $=\,\hat{x}[\iiint_\,\frac{\partial \phi}{\partial x}dxdydz]\,+\,\hat{y}[\iiint_\,\frac{\partial \phi}{\partial y}dxdydz]+\,\hat{z}[\iiint_\,\frac{\partial \phi}{\partial z}dxdydz]$

We would approximate above partial derivatives as constant, since their change is significantly small in infinitesimal space. For this reason, generally integral symbol can be dismissed, and result is:

$$\int_\,\phi\,d\sigma\,=\,\hat{x}\frac{\partial \phi}{\partial x}dxdydz\,+\,\hat{y}\frac{\partial \phi}{\partial y}dxdydz+\,\hat{z}\frac{\partial \phi}{\partial z}dxdydz$$

And, the below formula is

$$\int_\,d\tau\,\Rightarrow\,dxdydz$$

, As seen above, Grad(Φ) is

$\nabla\phi\,\,=\,\,\lim_{\int_\,d\tau \to 0}\frac{\int_\,\phi\,d\sigma}{\int_\,d\tau}$.

2) Div

When a vector function V is defined, the divergence of V, Div(V), is like below:

$$\nabla\cdot\,\mathbb{V}\,\,=\,\,\lim_{\int_\,d\tau \to 0}\frac{\int_\,\mathbb{V}\,\cdot\,d\sigma}{\int_\,d\tau}$$

Let us analysis above formula at origin O. ∫V·dσ on Cartesian Coordinate for each plane is expressed like below:

$$\int_\,\mathbb{V}\,\cdot\,d\sigma\,\,=$$ $$-\iint_\,[(V_x-\frac{\partial V_{x}}{\partial x} \frac{dx}{2})\hat{x}\,\cdot\,dydz\hat{x}]\,\,+\iint_\,[(V_x+\frac{\partial V_{x}}{\partial x} \frac{dx}{2})\hat{x}\,\cdot\,dydz\hat{x}]$$ $$-\iint_\,[(V_y-\frac{\partial V_{y}}{\partial y} \frac{dy}{2})\hat{y}\,\cdot\,dxdz\hat{y}]\,\,+\iint_\,[(V_y+\frac{\partial V_{y}}{\partial y} \frac{dy}{2})\hat{y}\,\cdot\,dxdz\hat{y}]$$ $$-\iint_\,[(V_z-\frac{\partial V_{z}}{\partial z} \frac{dz}{2})\hat{z}\,\cdot\,dxdy\hat{z}]\,\,+\iint_\,[(V_z+\frac{\partial V_{z}}{\partial z} \frac{dz}{2})\hat{z}\,\cdot\,dxdy\hat{z}]$$ $$=\int_\,(\frac{\partial V_{x}}{\partial x}+\,\,\frac{\partial V_{y}}{\partial y}+\,\,\frac{\partial V_{z}}{\partial z})\,d\,\tau$$

If integral symbol is dismissed,

$$=(\frac{\partial V_{x}}{\partial x}+\,\,\frac{\partial V_{y}}{\partial y}+\,\,\frac{\partial V_{z}}{\partial z})\,d\,\tau$$

And then

$$\int_\,d\tau\,\Rightarrow\,dxdydz$$

As we’ve seen before, Div(V) is

$$\nabla\cdot\,\mathbb{V}\,\,=\,\,\lim_{\int_\,d\tau \to 0}\frac{\int_\,\mathbb{V}\,\cdot\,d\sigma}{\int_\,d\tau}$$

3) Curl

When a vector function V is defined, the curl of V, Curl(V), is like below:

$$\nabla\times\,\mathbb{V}\,\,=\,\,\lim_{\int_\,d\tau \to 0}\frac{\int_\,d\sigma\,\times\,\mathbb{V}}{\int_\,d\tau}$$

Let us analysis above formula at origin O. ∫dσXV on Cartesian Coordinate for each plane is expressed like below:

(1)

$$\Leftarrow\,\,(dx\,\,direction)$$ $$:\,-\hat{x}\int_\,d\,yd\,z\,\,\times\,\,[\int_\,(V_y-\frac{\partial V_{y}}{\partial x}\,\frac{dx}{2})\hat{y}\,+\,\int_\,(V_z\,+\frac{\partial V_{z}}{\partial x}\,\frac{dx}{2}\hat{z})]$$ $$=\,-\int_\,(V_y-\frac{\partial V_{y}}{\partial x}\,\frac{dx}{2})\,dydz\,\hat{z}\,+\,\int_\,(V_z\,+\,\frac{\partial V_z}{\partial x}\,\frac{dx}{2})\,dydz\,\hat{y}$$ $$\Rightarrow\,\,(dx\,\,direction)$$ $$=\,\int_\,(V_y+\frac{\partial V_{y}}{\partial x}\,\frac{dx}{2})\,dydz\,\hat{z}\,-\,\int_\,(V_z\,-\,\frac{\partial V_z}{\partial x}\,\frac{dx}{2})\,dydz\,\hat{y}$$ $$\therefore,\,\Leftarrow+\,\Rightarrow\,=\,\frac{\partial V_{y}}{\partial x}\,dxdydz\hat{z}-\,\frac{\partial V_{z}}{\partial x}\,dxdydz\hat{y}$$

(2)

$$\swarrow\,\,(dz\,\,direction)$$ $$:\,-\hat{y}\int_\,d\,xd\,z\,\,\times\,\,[\int_\,(V_x-\frac{\partial V_{x}}{\partial y}\,\frac{dy}{2})\hat{y}\,+\,\int_\,(V_z\,+\frac{\partial V_{z}}{\partial y}\,\frac{dy}{2}\hat{z})]$$ $$=\,-\int_\,(V_x-\frac{\partial V_{x}}{\partial y}\,\frac{dy}{2})\,dxdz\,\hat{z}\,+\,\int_\,(V_z\,+\,\frac{\partial V_z}{\partial y}\,\frac{dy}{2})\,dxdz\,\hat{x}$$ $$\nearrow\,\,(dz\,\,direction)$$ $$=\,\int_\,(V_x+\frac{\partial V_{x}}{\partial y}\,\frac{dy}{2})\,dxdz\,\hat{z}\,-\,\int_\,(V_z\,-\,\frac{\partial V_z}{\partial y}\,\frac{dy}{2})\,dxdz\,\hat{x}$$ $$\therefore,\,\swarrow+\,\nearrow\,=\,\frac{\partial V_{z}}{\partial y}\,dxdydz\hat{x}-\,\frac{\partial V_{x}}{\partial y}\,dxdydz\hat{z}$$

(3)

$$\Downarrow\,\,(dy\,\,direction)$$ $$:\,-\hat{z}\int_\,d\,xd\,y\,\,\times\,\,[\int_\,(V_x-\frac{\partial V_{x}}{\partial z}\,\frac{dz}{2})\hat{x}\,+\,\int_\,(V_y\,+\frac{\partial V_{y}}{\partial z}\,\frac{dz}{2}\hat{y})]$$ $$=\,-\int_\,(V_x-\frac{\partial V_{x}}{\partial z}\,\frac{dz}{2})\,dxdy\,\hat{y}\,+\,\int_\,(V_y\,+\,\frac{\partial V_y}{\partial z}\,\frac{dz}{2})\,dxdy\,\hat{x}$$ $$\Uparrow\,\,(dy\,\,direction)$$ $$=\,\int_\,(V_x+\frac{\partial V_{x}}{\partial z}\,\frac{dz}{2})\,dxdy\,\hat{y}\,-\,\int_\,(V_y\,-\,\frac{\partial V_y}{\partial z}\,\frac{dz}{2})\,dxdy\,\hat{x}$$ $$\therefore,\,\Downarrow+\,\Uparrow\,=\,\frac{\partial V_{x}}{\partial z}\,dxdydz\hat{y}-\,\frac{\partial V_{y}}{\partial z}\,dxdydz\hat{x}$$

The addition of amount along the direction dx, dy, dz, this value would be (1) + (2) + (3). If integral symbol is dismissed,

$$[(\frac{\partial V_z}{\partial y}-\frac{\partial V_y}{\partial z})\hat{x}\,+\,(\frac{\partial V_x}{\partial z}-\frac{\partial V_z}{\partial x})\hat{y}\,+\,(\frac{\partial V_y}{\partial x}-\frac{\partial V_x}{\partial y})\hat{z}]dxdydz$$

So the Curl(V) is proved to be like below:

$$\nabla\times\,\mathbb{V}\,\,=\,\,\lim_{\int_\,d\tau \to 0}\frac{\int_\,d\sigma\,\times\,\mathbb{V}}{\int_\,d\tau}$$

4) Laplacian

When a scalar function Φ is defined, the laplacian of Φ, ∇^2_Φ, is like below:

$$\nabla^2 \phi\,=\lim_{\int_\,d\tau \to 0}\frac{\int_\,\nabla\phi\,d\sigma}{\int_\,d\tau}$$

(1)$\Leftarrow\,\,(dx\,\,direction)\,:\,\nabla\phi_x\,=\,$

$$(\frac{\partial \phi}{\partial x}-\frac{dx}{2}\frac{\partial^2 \phi}{\partial x^2})\hat{x}+(\frac{\partial \phi}{\partial y}-\frac{dy}{2}\frac{\partial^2 \phi}{\partial y^2})\hat{y}+(\frac{\partial \phi}{\partial z}-\frac{dz}{2}\frac{\partial^2 \phi}{\partial z^2})\hat{z},$$ $$d\sigma_x\,=\,-dydz\hat{x}$$ $$\Rightarrow\,\,(dx\,\,direction)\,:\,\nabla\phi_x\,=\,$$ $$(\frac{\partial \phi}{\partial x}+\frac{dx}{2}\frac{\partial^2 \phi}{\partial x^2})\hat{x}+(\frac{\partial \phi}{\partial y}+\frac{dy}{2}\frac{\partial^2 \phi}{\partial y^2})\hat{y}+(\frac{\partial \phi}{\partial z}+\frac{dz}{2}\frac{\partial^2 \phi}{\partial z^2})\hat{z},$$ $$d\sigma_x\,=\,dydz\hat{x}$$ $$\therefore,\,\Leftarrow+\Rightarrow\,=\,\frac{\partial^2 \phi}{\partial x^2}dxdydz$$

(2) $\swarrow\,\,(dz\,\,direction)\,:\,\nabla\phi_z\,=\,$

$$(\frac{\partial \phi}{\partial x}-\frac{dx}{2}\frac{\partial^2 \phi}{\partial x^2})\hat{x}+(\frac{\partial \phi}{\partial y}-\frac{dy}{2}\frac{\partial^2 \phi}{\partial y^2})\hat{y}+(\frac{\partial \phi}{\partial z}-\frac{dz}{2}\frac{\partial^2 \phi}{\partial z^2})\hat{z},$$ $$d\sigma_z\,=\,-dxdz\hat{y}$$ $$\nearrow\,\,(dz\,\,direction)\,:\,\nabla\phi_z\,=\,$$ $$(\frac{\partial \phi}{\partial x}+\frac{dx}{2}\frac{\partial^2 \phi}{\partial x^2})\hat{x}+(\frac{\partial \phi}{\partial y}+\frac{dy}{2}\frac{\partial^2 \phi}{\partial y^2})\hat{y}+(\frac{\partial \phi}{\partial z}+\frac{dz}{2}\frac{\partial^2 \phi}{\partial z^2})\hat{z},$$ $$d\sigma_z\,=\,dxdz\hat{y}$$ $$\therefore,\,\swarrow+\nearrow\,=\,\frac{\partial^2 \phi}{\partial y^2}dxdydz$$

(3)

$$\Downarrow\,\,(dy\,\,direction)\,:\,\nabla\phi_y\,=\,$$ $$(\frac{\partial \phi}{\partial x}-\frac{dx}{2}\frac{\partial^2 \phi}{\partial x^2})\hat{x}+(\frac{\partial \phi}{\partial y}-\frac{dy}{2}\frac{\partial^2 \phi}{\partial y^2})\hat{y}+(\frac{\partial \phi}{\partial z}-\frac{dz}{2}\frac{\partial^2 \phi}{\partial z^2})\hat{z},$$ $$d\sigma_y\,=\,-dxdy\hat{z}$$ $$\Uparrow\,\,(dy\,\,direction)\,:\,\nabla\phi_y\,=\,$$ $$(\frac{\partial \phi}{\partial x}+\frac{dx}{2}\frac{\partial^2 \phi}{\partial x^2})\hat{x}+(\frac{\partial \phi}{\partial y}+\frac{dy}{2}\frac{\partial^2 \phi}{\partial y^2})\hat{y}+(\frac{\partial \phi}{\partial z}+\frac{dz}{2}\frac{\partial^2 \phi}{\partial z^2})\hat{z},$$ $$d\sigma_y\,=\,dxdy\hat{z}$$ $$\therefore,\,\swarrow+\nearrow\,=\,\frac{\partial^2 \phi}{\partial z^2}dxdydz$$

If (1) + (2) + (3), the result is like:

$$\nabla\,\phi\,d\sigma\,=\,(\frac{\partial^2 \phi}{\partial x^2}\,+\,\frac{\partial^2 \phi}{\partial y^2}\,+\frac{\partial^2 \phi}{\partial z^2})dxdydz$$

If integral symbol is dismissed and divided by d(tau),

$$\nabla^2 \phi\,=\lim_{\int_\,d\tau \to 0}\frac{\int_\,\nabla\phi\,d\sigma}{\int_\,d\tau}$$

We’ve introduced the expression of Grad, Curl, Div, and Laplacian for cartesian coordinates and have just finished to find out whether they’re actually right.

• References
  1. Mathematical Methods for Physicists, 1st ed., ARFKEN & WEBER, ch.1, Vector analysis, p. 58<
  2. In the same book, p. 63

Twitter  facebook  Google+ 

Contact

Name: * Email Address: * Message: *
* indicates a required field