1) Introduction to SLAM - Probabilistic SLAM

Engineering - SLAM · 20 Nov 2019 1. What is SLAM?

In robotics, SLAM(Simultaneous Localization And Mapping) means the process where a mobile robot 1) builds a map of an unknown environment 2) while at the same time being localized relative to this map.

To localize the position, the information of surrounding is essential. However, to make a map around robot obtained by itself, there should be a knowledge about the accurate location. Therefore these problems are indispensable. SLAM performs simultaneously both mapping and position estimation to solve this kind of a problem.

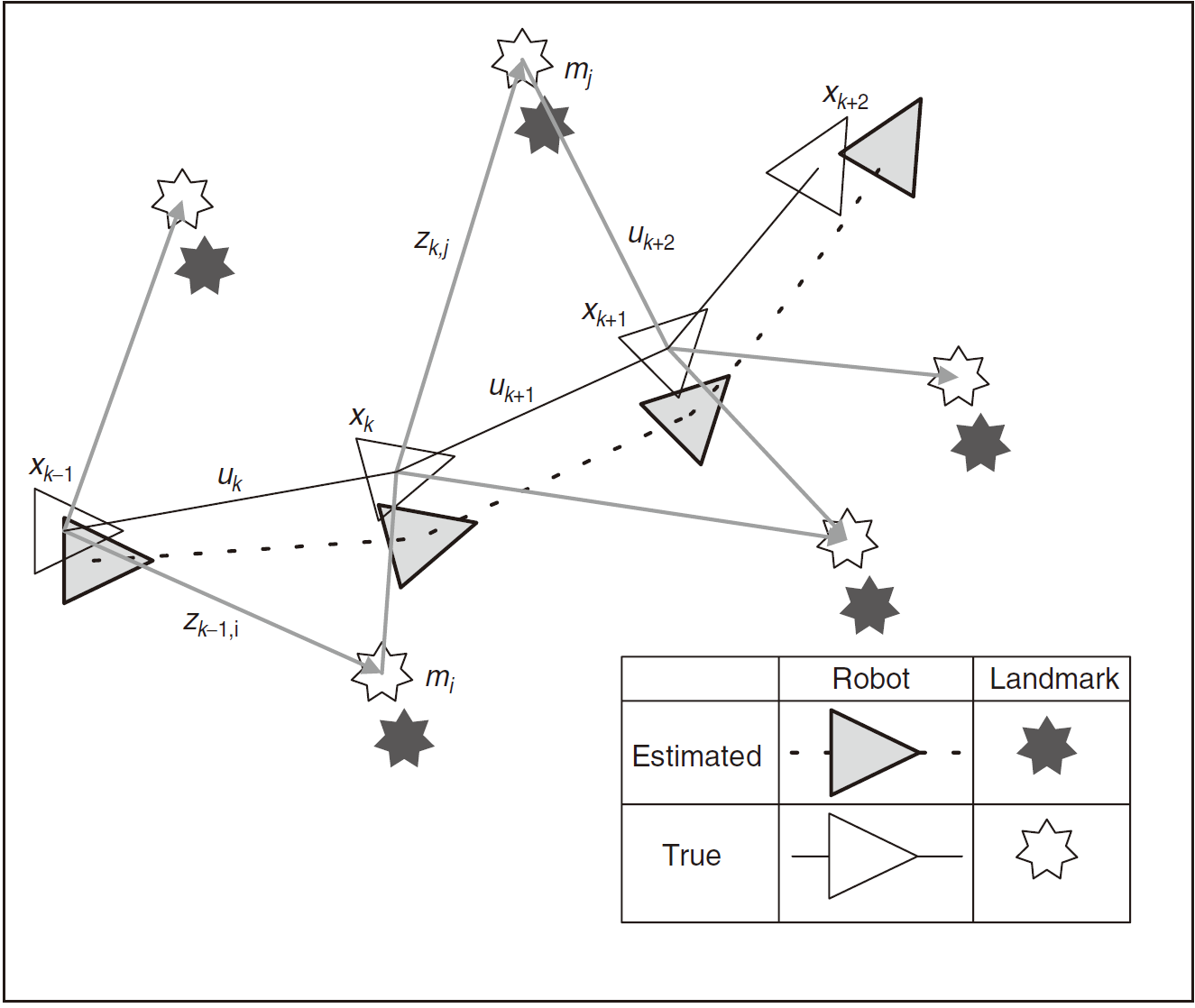
useful image

[Fig 1. The essential SLAM problem. A simultaneous estimate of both robot and landmark locations is required. The true locations are never known or measured directly. Observations are made between true robot and landmark locations.] 2. Formulation and Structure of the SLAM Problem

SLAM is a process by which a mobile robot can build a map of an environment and at the same time use this map to deduce its location. In SLAM, both the trajectory of the platform and the location of all landmarks are estimated online without the need for any a priori knowledge of location. To determine whether act or not, it needs for robot to think(or act with program) according to probability theory, especially in this case, ‘markov process.’

Preliminaries

$\textbf{x}_k:$ the state vector describing the location and orientation of the vehicle

$\textbf{u}_k:$ the control vector, applied at time $k−1$ to drive the vehicle to a state $\textbf{x}_k$ at time $k$

$\textbf{m}_i:$ a vector describing the location of the $i$th landmark whose true location is assumed time invariant

$\textbf{z}_{ik}:$ an observation taken from the vehicle of the location of the ith landmark at time $k$. When there are multiple landmark observations at any one time or when the specific landmark is not relevant to the discussion, the observation will be written simply as $\textbf{z}_k$ .

In addition, the following sets are also defined:

$\textbf{X}_{0:k} = ({\textbf{x}_0 , \textbf{x}_1, \dots , \textbf{x}_k}) = ({\textbf{X}_{0:k-1},\textbf{x}_k }):$ the history of robot/vehicle locations

$\textbf{U}_{0:k} = ({\textbf{u}_1 , \textbf{u}_2, \dots , \textbf{u}_k}) = ({\textbf{X}_{0:k-1},\textbf{x}_k }):$ the history of control input

$\textbf{m} = ({\textbf{m}_1 , \textbf{m}_2, \dots , \textbf{m}_n}):$ the set of all landmarks

$\textbf{Z}_{0:k} = ({\textbf{z}_1 , \textbf{z}_2, \dots , \textbf{z}_k}) = ({\textbf{Z}_{0:k-1},\textbf{z}_k }):$ the set of all landmark observations.

3. Probabilistic SLAM and Its Structure

In probabilistic form, the simultaneous localization and map building (SLAM) problem requires that the probability distribution

$P(\textbf{x}_k, \textbf{m}|\textbf{Z}_{0:k}, \textbf{U}_{0:k}, \textbf{x}_0) \tag{1}$

be computed for all times $k$.¹ $P$ describes the joint posterior density of the landmark locations and vehicle state (at time k) given the recorded observations and control inputs up to and including time k together with the initial state of the vehicle. Researcher or user of the probabilistic SLAM would think like that: a recursive solution to the SLAM problem is desirable.

$\begin{cases}The\ observation\ model: & P(\textbf{z}_k|\textbf{x}_k,\ \textbf{m}) & (2) \\ The\ motion\ model: & P(\textbf{x}_k|\textbf{x}_{k-1},\ \textbf{u}_k) & (3) \end{cases}$

For the observation model, it is reasonable to assume that once the vehicle location and map are defined, observations are conditionally independent given the map and the current vehicle state, meanwhile the state transition is assumed to be a Markov process in which the next state $\textbf{x}_{k}$ depends only on the immediately preceding state $\textbf{x}_{k−1}$ and the applied control $\textbf{u}_{k}$ and is independent of both the observations and the map. So now what we would do next? There are two steps researcher or user can do.

$\begin{matrix}\textbf{Time-update(prediction)}: \\ P(\textbf{x}_k, \textbf{m}|\textbf{Z}_{0:k-1}, \textbf{U}_{0:k}, \textbf{x}_0)\ = \ \int \underset{motion \ model}{\underline{P(\textbf{x}_{k}|\textbf{x}_{k-1}, \ \textbf{u}_k)}} \ \times \ P(\textbf{x}_{k-1}, \textbf{m}|\textbf{Z}_{0:k-1}, \textbf{U}_{0:k-1}, \textbf{x}_0) \ d\textbf{x}_{k-1} \tag{4} \end{matrix}$ $\begin{matrix}\textbf{Measurement-update(correction)}: \\ P(\textbf{x}_k, \textbf{m}|\textbf{Z}_{0:k}, \textbf{U}_{0:k}, \textbf{x}_0)\ = \ \frac{\underset{observation \ model}{\underline{P(\textbf{z}_k | \textbf{x}_k, \ \textbf{m})}} P(\textbf{x}_k, \ \textbf{m}|\textbf{Z}_{0:k-1}, \ \textbf{U}_{0:k}, \ \textbf{x}_0)}{P(\textbf{z}_k | \textbf{Z}_{0:k-1}, \ \textbf{U}_{0:k})} \tag{5} \end{matrix}$

In next article, we’re now about to see what is markov process, the history of SLAM, and re-visit Probabilistic SLAM with these materials.

References

Hugh Durrant-Whyte, Tim Bailey, IEEE Robotics & Automation Magazine, June 2006, Simultaneous Localization and Mapping: Part 1
http://jinyongjeong.github.io/2017/02/13/lec01_SLAM_bayes_filter/ (2019.11.23)
https://www.cs.cmu.edu/~motionplanning/lecture/Chap9-Bayesian-Mapping_howie.pdf

$\matrix{P(a|b) & = \frac{(b|a) \ p(a)}{p(b)} \\ p(x,y) & = p(x|y) \cdot \ p(y) \\ & = p(y|x) \cdot \ p(x) \\ p(a|b,c) & = \frac{p(b|a,c) \ p(a|c)}{p(b|c)}}$

Note that ↩