Categories

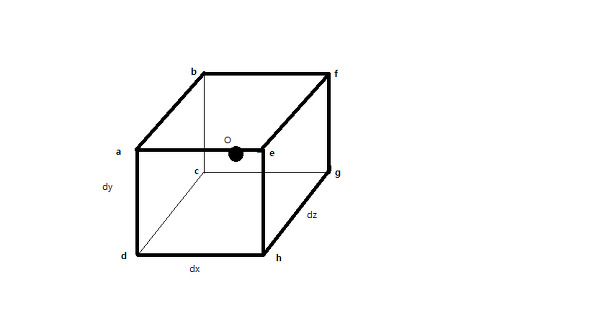
4) The basic of tensor algebra (1) - Vector revisited

Tensor is, simply speaking, the expansion of vector. More strictly speaking, The tensor inherits the property of the vector, because the tensor is the superordinate concept of the vector. Once we took the subject of this article as ‘vector revisited’, let us start from the notion of the vector space. Wait, What is the vector, then?

Vector is the...

3) Why tensor? (2) Mechanics of materials

• • When the engineer and the scientist want to analyze the stress for a declined or inclined surface, he/she would often use the Mohr’s circle. First, we start from the stress transformation diagram.

By the...

2) Why tensor? (1) Dynamics of a particle in Curvilinear Motion

We’ve got seen the gradient, divergence, curl, and laplacian of a vector field or scalar function. If you are in engineering course, some of you’re going to take the engineering dynamic course.

First, we would be informed about general curvilinear motion of a particle along a certain path. Let a length of moving path for a particle from the origin...

1) Gradient, Divergence, Curl and Laplacian

I took the work I’d done 5 yrs ago.

cf) I would inform you the calculation is done in what surface once.

I will use just a picture to explain you Grad, Div, Curl, and Laplacian.

1) Grad

When a scalar...

2) Valve Selection Criteria - (1) Valve Coefficients and Three Principal Types of Flow Type

When you design the pneumatic or hydraulic system, according to the Bernoulli’s equation in compressible flow situation

where $g$ is the gravity acceleration constant, $h$ is the height of the fluid line from the reference point, $\rho$ is the density property of fluid being analyzed, and $\int dP$...

1) definition and classification by function

1] Valves: Mechanical devices specifically designed to direct, start, stop, mix, or regulate the flow, pressure, or temperature of a working fluid. Here is a type of valves - ball valves. ¹

1) Embedded Systems

Processor: CPU - ALU(Arithmetic and Logic Unit), CU(Control Unit), Register and Internal Bus

• Register The Temporal Device of memory that saves the data temporarily in processor - General Purpose Register - Control Register(Program Counter)- Status Register(Expresses the status of processor): Physically structured with the Latches and Flip-Flop
• ALU(Arithmetic and Logic Unit): Arithmetic, Logic, Compliment, and...

6) Bending/Transverse Stress

Bending is somewhat longitudinal phenomenon. In that point one can get a longitudinal reference axis and members that are slender, called as Beam whose support loading is exerted on perpendicular to reference axis.

…

5) Torsinoal Load

• Torsional Deformation

Consider a shaft $AB$ subjected at $A$ and $B$ to equal and opposite torques $\mathbf{T}$ and $\mathbf{T’}$.We pass a section perpendicular to the axis of the shaft through some arbitrary point $C$ [Fig. 5.1.].

4) Axial Load

We have shown that the mathematical relationship between stress and strain depends on the type of material from which the body is made. In particular, if the material behaves in a linear elastic manner, then Hooke’s law applies, and there is a proportional relationship between stress and strain....

3) Mechanical Properties of Materials - From The Ductility and Brittleness

Ductile Materials: Any material that can be subjected to large strains before it fractures is called a ductile material. Mild steel, as discussed previously, is a typical example. Engineers often choose ductile materials for design because these materials are capable of absorbing shock or energy, and if they become overloaded, they will usually exhibit large deformation...

2) Stress and Strain - Strain

When an excessive stress is applied to the body of certain material, the shape of the body would be changed. It is called to Deformation. The deformation includes the case of yielding, necking, and rupture, etc., but in this chapter yielding is the principal subject. In a general sense, the deformation will not be uniform throughout...

1) Stress and Strain - Stress

Stress means the force acting on the unit area, such as $\sigma\,=\,\frac{F}{A} [\frac{N}{m}]\,=\,[Pa]$ where $F\,:\,Force,\,A\,=\,Area$.

Strain means the difference between the initial length and final length for compared to the initial length, such as $\epsilon\,=\,\frac{L_0\,-\,L_f}{L_0}$. where $L_0$ is initial length of a specimen of a certain material, and $L_f$ is final length of the specimen.

The...

1) Introductions for the heat and mass transfer

Why the mechanical engineer should know how the heat and mass is transferred? for mechanical engineers, it is essential for them to analyze:

• how the reaction between the mechanical components
• how the individual component or subsystem endures long for the given conditions
• how much mechanical power transmission occurs by heat and mass transfer

However, we don’t know exactly...

1) The basic of linear algebra (1) - what is the linear algebra?

There is the historical fact that in china, the equivalent procedure for the gauss elimination is used as early as 200 BC. The main use of the linear algebra is to solve the simultaneous equation system. In Nine Chapters of the Mathematical Art (九章算術), whose early version of this book was burnt by the...

1) Machining operations - cutting tool materials (1)

The recommended cutting feeds and speeds in the accompanying tables are given for high-speed steel, coated and uncoated carbides, ceramics, cermets, and polycrystalline diamonds. More data are available for HSS and carbides because these materials are the most commonly used. Other materials that are used to make cutting tools are cemented oxides or ceramics, cermets, cast...

The critical frequency of the helical spring

The governing equation for the translational vibration of the spring placed between two flat and parallel plates is

Assume that $\rho$ is...

1) Introduction to SLAM - Probabilistic SLAM

In robotics, SLAM(Simultaneous Localization And Mapping) means the process where a mobile robot 1) builds a map of an unknown environment 2) while at the same time being localized relative to this map.

To localize the position, the information of surrounding is essential. However, to make a map around robot obtained by itself, there should be...